Langkah2 Model Panel Data

Secara ringkas step-stepnya Panel Data (Statis) adalah sebagai berikut:

1. Estimasi dengan Fixed Efect.

2. Uji Chow-test (Pool Vs Fixed efek).
(a). Jika Ho diterima, maka model pool (common). (selesai sampai disini).
(b). Jika Ho ditolak, maka model Fixed efek. (teruskan step 3)

3. Estimasi dengan Random Efek.

4. Uji Hausman (random Vs Fixed).

(a). Jika Ho: diterima, maka model random efek (selesai sampai disini).
(b). Jika Ho: ditolak, maka model fixed efek (lanjutkan step 5)

5. Uji LM test :adanya herosedastisity antar kelompok individu (crossection).

Ho: Homosedastik
H1: Heterosedastik

(a) Jika Ho diterima, maka model homosedastik (selesai)
(b) Jika Ho ditolak, maka model heterosedastik. Solusi: dg Crossection Weight (dan lanjutkan step 6)

6. Uji LR test: adanya heterosedastik dan otokorelasi antar kelompok individu (crossection).

Ho: Struktur heterosedastik
Ho: struktur SUR

(a). Jika Ho diterima, maka model herosedastik. Solusi: dg Crossection Weigth (sama dg 5.b)
(b). Jika Ho ditolak, maka model SUR. Solusi: dg Crossection SUR.

Untuk Cara penggunaan Eviews lebih detil lihat:
(a). Bila setting struktur data “unstack” (object–>Pool) klik tulisan Panel data.
(b). Bila setting struktur data “stack” (object–>panel) klik tulisan Panel data dg Eviews.

Read More......

Dynamic Panel Data

Tulisan ini sangat ringkas, hanya sebagai panduan secara umum berkaitan dengan model dynamic Panel Data dikarenakan ada beberapa pertanyaan dari para pengunjung blog ini.

Banyak perilaku ekonomi mempunyai hubungan dynamic (dinamis), misalnya permintaan dinamis pada gas alam, permintaan dinamis pada bensin dan listrik rumah tangga dan persamaan dinamis pada wages. Analisis Panel Data untuk persoalan tersebut menggunakan model dynamic panel data.

Model Dynamic Panel Data sebagai berikut.

di mana uit adalah error dengan rata-rata nol dan varians tertentu. zit adalah matrik kumpulan variabel eksogen dan yit-1 adalah variabel predetermine (variabel eksogen berasal dari variabel endogen). Untuk mengatasinya beberapa model diajukan sbb.

1. Model AR(1)

Model AR(1) ini, apabila kita mengasumsikan ortogonality condition yaitu variabel eksogen (yit-1 dan zit) tidak berkorelasi uit. Maka kita dapat gunakan estimator OLS (fixed effect) atau GLS (random effect). (Wooldridge, Econometric Analysis of Crossection and Panel Data)

2. Model First Differencing

Apabila Model AR(1) tersebut, kita duga terjasi pelanggaran asumsi ortogonality condition yaitu variabel eksogen (yit-1 dan zit) berkorelasi uit. Maka kita model tersebut ditranformasi dengan first differencing. Dan selanjutnya dapat kita gunakan estimator OLS atau GLS. (Wooldridge, Econometric Analysis of Crossection and Panel Data)

3. Model Instrumen Variabel (2SLS)

3.a Model AR(1) - Lag Endogen

Model ini mengagap bahwa variabel yit-1 berkorelasi dengan uit, sehingga dapat diselesaikan dengan menggunakan instrumen variabel untuk menggantikan yit-1 dan dilakukan 2SLS.

Step 1: Regres : yit-1 on ∆yit-1 dan estimate yit-1 sebut saja yit-1Cap
Step 2: Regres : yit on yit-1Cap zit



3.b. Model Lag Endogen & Eksogen.

Model ini mengagap bahwa variabel eksogen (yit-1 dan zit) berkorelasi dengan uit, sehingga dapat diselesaikan dengan menggunakan instrumen variabel untuk menggantikan yit-1 dan zit, kemudian dilakukan 2SLS. Anderson & Hsiao (1981) menyarankan yit-2 sebagai intrumen dari ∆yit-1 . Intrument tersebut tidak akan berkorelasi dengan ∆uit selama error tersebut tidak mengandung serial correlation.

Step 1: Regres : ∆yit-1 on yit-2 dan estimate ∆yit-1 sebut saja ∆yit-1Cap
Regres : ∆zit on zit-1 dan estimate ∆zit sebut saja ∆zitCap

Step 2: Regres : ∆yit on ∆yit-1Cap ∆ zitCap

3. Model Arellano - Bond



xit=stricly exogenous variable (matrix)
zit=predtermine variable (matrix)
ci =random effect, iid,
uit=error, iid

Solusi Dynamic Panel data Model AR(1) dengan 2SLS tersebut menurut Arellano menghasilkan estimasi yang konsisten namun ada kemungkinan tidak efesien (tidak varians minimum) oleh karena tidak mempertimbangkan moment condition yang ada. Arellano-Bond menyarankan ∆yit-2 sebagai intrumen dari ∆yit-1. Prosedur ini menghasilkan estimator lebih efisien daripada prosedur Aderson & Hsiao.

Oleh karena itu, Arellano-Bond mengajukan estimator dengan menggunakan GMM untuk estimasi .

Catatan:

Estimator lainnya, diajukan oleh Ahn & Schmidt (1995) yang menambahkan aspek nonlinier moment restiction yang tidak dibahas oleh Arellano & Bond (1991) pada GMM estimatornya.

Arellano & Bover (1995) memperbaiki estimator Arrellono & Bond (1991) dengan situasi apabila terdapat variabel eksogen yang bersifat endogen pada persamaan sebelah kanan (atau dengan kata lain terdapat adanya korelasi beberapa variabel eksogen dengan errornya. Berbeda dengan Arellano & Bond (1991), Arellano & Bover (1995) tidak melakukan transformasi first difference, namun menggunakan transformasi (pemisahan variabel-persamaan sebelah kanan menjadi ekosogen murni dan eksogen yang bersifat endogen) sedemikian sehingga kondisi ortogonallity terpenuhi. Estimastor ini di samping menggunakan GMM juga mengaplikasi 3SLS untuk estimasi intrumen variabelnya.

Blundell & Bond (1998) mengajukan estimator dengan situasi di mana T (variabel series) terbatas) kecil dan stasioner. Berbeda dengan Arellano & Bond (1991), Blundell & Bond menyanrakan intrumen variabel yit-2 sebagai intrumen dari ∆yit-1. Blundel & Bond (1998) mengklaim estimatornya lebih efesien dibandingkan dengan estmator Arellano & Bond (1991) sengan kondisi sample kecil dan stasioner.

Bersambung ..............

Read More......

Panel Data dg Eviews

Penggunaan Eviews (minimal versi 5.1) untuk analisis Panel Data dapat menggukana struktur data "unstack" atau "stack". Struktur data "unstack" mengunakan object "POOL" dan data berdasarkan per series, misalkan satu variabel pendidik menjadi 10 variabel (karena ada 10 crossection-individu: educ_kab1, educ_kab2,..., educ_kab2). Penggunaan Panel data dengan "unstack" sudah dijelaskan di Blog ini pada tulisan klik Panel Data. Sedangkan struktur data "stack"-tersusun menumpuk ke bawah, mulai dari crossection-individu dan series.

Pada tulisan kali ini berisi tentang Panel Data menggunakan Eviews dengan setting data "stack".

1. SETTING DATA PANEL (STACK)

Data yang akan digunakan adalah WAGEPAN yang diambil dari buku: Jeffrey M. Wooldridge, Econometrict Analysis of Cross Section and Panel data, 2002, halaman 296. Sebagian dapat ditampilkan sbb:

Terlihat bahwa struktur data tersebut adalah “Stack” tersusun menumpuk ke bawah.

Secara lengkap data tersebut terdiri dari: NR(code individu-crossection), year (tahun-series), wage (gaji), educ (pendidikan-year of schooling), black (ras-putih 0, hitam 1), hisp (Hispanic-keturunan Spanish 1, bukan 0), exper (pengalaman kerja dlm tahun), married (Status-menikah 1, belum 0), union (1-serikat kerja, 0-tidak). Data cross section sebanyak 545 individu dan data series 8 tahun (1980-1987)

Memasukan data execel ke dalam Eviews sbb:

• Buka Eviews (min 5.1) dan create workfile, yaitu klik-->New-Workfile. Isilah Workfile structure, Frequency ..dst seperti di bawah ini dan klik-->OK.

• Workfile masih Untitle, lakukan save workfile : klik-->File-Save as-(ketik nama file-Wagepan)

• Untuk meng-input data excel (workpan.xls) ke dalam Eveiws, yaitu dalam Workfile Eview, siapkan object group: Klik-->Object-New Object-Group(pilih type of object)-latihan(Name of object-ganti untitle dg latihan).

• Kemudian Buka file wagepan.xls dan copy semua data (Ctrl-A, Ctrl-C). Kembali ke Workfile Eviews buka pada Group-Latihan tadi, dan klik ujung kolom disamping obs sehingga berwarna hitam seperti di atas, lalu Ctrl-V (paste dari copy excel)

• Kemudia, simpan kembali file tersebut: klik-->File-Save.

Dengan langkah-langkah tersebut data setting dalam bentuk "stack" telah siap untuk di analisis panel data lebih lanjut.

1. MODEL PANEL

Dalam model Panel data ini, independen variabel adalah educ. black, hispan, exper, exper2, maried, union dan variabel dependen adalah wage. Dalam model ini menduga bahwa gaji seorang dipengaruhi oleh tingkat pendidikan, ras, pengalaman kerja, status perkawinan dan serikat kerja. Namun demikian, sebenarnya ada faktor lain yang mempengaruhi gaji seseorang ialah Ability-kemampuan yang merupakan unobserved variabel yang dicerminkan sebagai individual efek- Ci dalam model diatas. Sebenarnya Ci masuk dalam residual (eit=uit + Ci) dan keunggulan panel data dapat melakukan meng-ekstrak/ mengeluarkan Ci-individual efek dari residualnya.

Model Fixed Effect atau Pool

Estimasi Model Fixed Effect tidak membolehkan suatu variabel yang tidak berubah setiap tahunnya, yaitu variabel Black (warna kulit) dan Hispanic. Oleh karena itu, ke dua variabel tersebut tidak diikut sertaka dalam suatu model ini.

Estimasi model Fixed Effect (FEM) dengan Eviews: klik--> Quick-Estimate Equation dan tuliskan variabel dependen dan independen. Dan Pilih Panel Option Crossection Fixed.

dan hasil estimasi koefisien Fixed Effect diperoleh:


sehingga persamaan tsb adalah: LWAGE = 1.064879845 + 0.1168466917*EXPER - 0.004300889064*EXPERSQ + 0.04530331751*MARRIED + 0.08208713417*UNION.

Simpan persamaan tersebut dg nama Fixed: klik--> Name: Fixed

sedangkan untuk mencari individul efek dari persamaan ini, ialah klik-->View-Fixed/Random Effect-Cross section effect.

...............................................

Pertanyaannya adalah apakah pada model fixed effect koefisien (cross-section)-nya berbeda saat atau tidak berbeda (model Pool).

Pengujian yang dilakukan menggunakan Chow-test atau Likelihood ratio test, yaitu:
H0: model mengikuti Pool
H1: model mengikuti Fixed.

Statistik Uji F atau Chi-Kuadrat.

Dengan Evews, klik--> View-Fixed/Random Effect Testing-Redundant Fixed Effect
maka dipeoleh hasil sebagai berikut.
hasil tersebut menunjukkan baik F test maupun Chi-square signifikan (p-value 0,000 lebih kecil dari 5%) sehigga H0 ditolak dan H1 diterima, maka model mengikuti Fixed Effect.

Model Random Effect atau Fixed Effect

Selanjutnya kita coba estimasi Model Random Effect.

Estimasi model Random Effect (REM) dengan Eviews: klik--> Quick-Estimate Equation dan tuliskan variabel dependen dan indpenden, sama seperti contoh di atas. Dan Pilih Panel Option Crossection Random. Hasilnya adalah sebagai berikut.

sehingga persamaan tsb adalah: LWAGE = 1.067721185 + 0.1175546195*EXPER - 0.004793499502*EXPERSQ + 0.07491061976*MARRIED + 0.100072838*UNION

Simpan persamaan tersebut dg nama Fixed: klik--> Name: Random

Sedangkan untuk mencari individul efek dari persamaan ini, ialah klik-->View-Fixed/Random Effect-Cross section effect.

Pertanyaannya adalah apakah model sesuai dengan Random Effect atau Fixed Effect.

Pengujian yang dilakukan menggunakan Hausman test, yaitu:
H0: model mengikuti Random Effect
H1: model mengikuti Fixed Effect.

Statistik Uji Hausman.

Dengan Evews, klik--> View-Fixed/Random Effect Testing-Hausman Test, maka dipeoleh hasil sebagai berikut.

Hasil pengujian tersebut signifikan (p-value 0,000 kurang dari 5%), sehingga H0 ditolak dan H1 diterima. Oleh karena itu, model mengikuti Fixed Effect.

Bersambung.....
Berkaitan dengan pelanggaran asumsi otokorelasi dan homosedastic

Read More......

Welcome

Kajian ekonometrika sangat menarik perhatian kita baik para akademisi, decision maker, maupun private sektor untuk memahami fenomena ekonomi & finansial yang telah, sedang dan akan terjadi. Alat yang digunakan untuk memahami gejala tersebut adalah ekonometrika yang mencakup:

Model Regresi Linier:

• Estimasi Model Regresi Linier dg OLS dan Maximum Likelihood
• Statistik Uji t dan F dlm Model Regresi Linier dg Eviews
• Pengujian Multikolinieritas
• Pengujian Homosedastisitas
• Pengujian Otokorelasi

Model Regresi Non Linier:

• Estimasi Model Regresi Non-Linier dg OLS dan Maximum Likelihood
• Estimasi Model Regresi Non Linier dg Genetic Algoritma

Time Series:

• Stasioneritas
• ARIMA, ARCH-GARCH
• Statistik Uji z dan T pada Model GARCH/ EGARCH dg Eviews
• Cointegration, VAR, VEC, ECM
• Aplikasi VAR: Currency Crisis Effect on the Stock Market- A Case Study in Indonesia

Panel Data:

• Langkah Langkah Panel Data
• Panel data
• Panel Unit Root Test
• Hausman Test pada Panel Data
• Panel data (Stack structure) dg Eviews
• Dynamic Panel Data

Persamaan Simultan:

• Persamaan Simultan dg estimator two stages least square.
• Full Information Maximum Likelihood utk estimasi persamaan simulatan

Banyak paket program- program ekonometrik yang tersedia antara lain EVIEWS, STATA, SPSS dll sebagai alat untuk komputasi ekonometrika.
Kami mengundang Anda sekalian untuk mendiskusikan tentang ekonometrika terutama pada aplikasinya.
Salam

Read More......

Hausman Test pada Panel Data

Pada model Panel data kita ingin mengetahui apakah model tersebut fixed effect atau random effect. Model fixed effect mengasumsikan independen variabel berkorelasi dengan error-nya sedangkan random effect sebaliknya.

Model Panel data dengan Fixed Effect diestimasi dg OLS, sedangkan Random Effect diestimasi dengan GLS (generalized Least Square).

Untuk melihat apakah model mengikuti random effect atau fixed effect digunakan Uji Hausman:

Ho : random effect
H1 : Fixed effect.

Dengan mengunakan Eviews 5.1 kita dapat menghitung statistik uji tersebut dan nilai p-value nya sehingga dapat diputuskan model mana yang cocok (random/ fixed effect). Prosedur secara detail dapat dilihat pada tulisan sebelumnya (Panel Data) silahkan download sebelumnya.

Jika kita hanya punya program Eviews 5 dan versi sebelumnya, maka ini yang menjadi persoalan. Kita harus membuat Program untuk menghitung statistik uji Hausman. Namun, program tersebut dapat kita peroleh dari komplemen program Eviews tersebut.

Contoh Program Hausman test.
--------------------------------------------------------------------------
' hausman test for fixed versus random effects
' revised for version 5.0 (5/25/2004)

'change path to program path
%path = @runpath
cd %path

' load workfile
load grunfeld '(Ctt: ganti dg nama workfile yang sedang dikerjakan)

' set sample
smpl @first 1947 '(Ctt: hilangkan)

' estimate fixed effects and store results
pool1.ls(cx=f) log(inv?) log(val?) log(cap?) '(Ctt: ganti dg varibel dept & indept yg dianalisis)
vector beta = pool1.@coefs
matrix covar = pool1.@cov

' keep only slope coefficients
vector b_fixed = @subextract(beta,1,1,2,1) '(jika 3 var dept ganti dg (beta,1,1,2,1,3,1) dst)
matrix cov_fixed = @subextract(covar,1,1,2,2) '(jika 3 var dept ganti dg (covar,1,1,2,2,3,3) dst)


' estimate random effects and store results
pool1.ls(cx=r) log(inv?) log(val?) log(cap?) '(Ctt: ganti dg varibel dept & indept yg dianalisis)
beta = pool1.@coefs
covar = pool1.@cov

' keep only slope coefficients
vector b_gls = @subextract(beta,2,1,3,1) '(jika 3 var dept ganti dg (beta,2,1,3,1,4,1) dst)
matrix cov_gls = @subextract(covar,2,2,3,3) '(jika 3 var dept ganti dg (covar,2,2,3,3,4,4) dst)

' compute Hausman test stat
matrix b_diff = b_fixed - b_gls
matrix var_diff = cov_fixed - cov_gls
matrix qform = @transpose(b_diff)*@inverse(var_diff)*b_diff

if qform(1,1)>=0 then
' set table to store results
table(4,2) result
setcolwidth(result,1,20)
setcell(result,1,1,"Hausman test for fixed versus random effects")
setline(result,2)

!df = @rows(b_diff)
setcell(result,3,1,"chi-sqr(" + @str(!df) + ") = ")
setcell(result,3,2,qform(1,1))
setcell(result,4,1,"p-value = ")
setcell(result,4,2,1-@cchisq(qform(1,1),!df))
setline(result,5)

show result
else
statusline "Quadratic form is negative"
endif

-------------------------------------------------------------------------------------

Contoh program Hausman dan data set bisa didownload (Program dan Data). Anda dapat mencoba run program tersebut. Copy kedua file tersebut dan masukan pada sub-direktori yang sama dan selanjutnya Run dg Eviews.

Selah Anda berhasil mencoba contoh tersebut. Silahkan Anda coba dengan workfile yang akan dianalisis dan edit program Hausman.prg sesuai dengan catatan warna merah dan biru diatas.

Rumit bukan? salah sedikit saja bisa error.

Nah.... bagaimana dengan cara manual dengan Excel, yaitu langkah langkah sbb:

1. Run dg Eviews model FE dan copy koefisien-nya (tanpa konstanta) dan paste di excel. dan copy juga matrix covarian-nya dan paste ke excel.
   
2. Run dg Eviews model RE dan copy koefisien-nya (tanpa konstanta) dan paste di excel. dan juga copy juga matrix covarian-nya dan paste ke excel.
   
3. Kurangkan koefisien- koefisien (FE-RE) demikian pula Covariannya (FE-RE).
4. Hitung Statistik Uji Hausman (lihar rumus diatas): [transpose koef(FE-RE)] dikali [inverse covarian (FE-RE)] dikali [koef(FE-RE)].
5. Bandingkan nilai tersebut dg tabel Chi-kuadrat. Jika nilai hitung > nilai tabel, maka tolak Ho dan terima H1.

Silahkan download untuk tamplate Excel ini (untuk 4 variabel independen dan bisa disesuaikan beberapa variabel saja).

Read More......

Statistik Uji t dan F pada Model Regresi Linier dg Eviews

Beberapa hari yang lalu ada pertanyaan dari Sohib Mahasiswa di Perguruan Tinggi di Surabaya tentang Pengertian Statistik Uji t, Statistik Uji F, Statistik Uji z dan Statistik Uji T. Saya mencoba menjawab secara ringkas berkaitan dengan hal itu.

Model Regresi Linier:

Misalkan Model Regresi Multiple yaitu:

Log(M1) = a0 + a1Log(IP) + a2TB3 + e

dimana M1(Money Supply), IP(Industrila Production), dan TB3(Tresury Bill 3month).

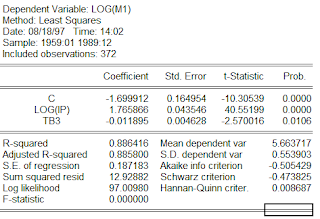
Dengan mengunakan Eviews untuk estimasi koefisien a0, a1, a2 menggunakan metoda OLS diperoleh output:

terlihat bahwa koefisien a1=1,765866 mengandung arti bahwa kenaikan 1 persen Industrial Production akan meningkatkan money supply sebesar 1,76 persen. Apakah IP dapat mempengaruhi M1? Untuk menyakinkan pengaruh tersebut, perlu diuji Ho : a1=0 dan diperoleh Statistik Uji t sebesar 40.55199 atau dengan p-value sebesar 0,000. Dengan kita ambil tingkat kesalahan (alpa 5%), maka kita tolak Ho karena p-value (0,000) lebih kecil dari tingkat kesalahan (alpa 5%). Dengan demikian kita yakin bahwa a1 tidak sama dg nol atau IP mempunyai pengaruh terhadap M1.

Demikian pula jika kita akan menguji koefisien a0 atau a2 secara masing- masing menggunakan Statistik Uji t.

Pertanyaan selanjutnya apakah IP dan TB3 secara bersama-sama mempengaruhi M1, maka kita akan menguji signifikasi koefisien a1 dan a2 secara bersama-sama (Ho: a1=a2=0). Statistik Uji yang digunakan adalah Statistik Uji F dengan nilai p-value =0,0000. Dengan kita ambil tingkat kesalahan (alpa 5%), maka kita tolak Ho karena p-value (0,0000) lebih kecil dari tingkat kesalahan (alpa 5%). Dengan demikian kita yakin bahwa IP dan TB3 secara bersama-sama mempunyai pengaruh terhadap M1 (cat: karena koef IP dan TB3 signifikan).

Bagaimana dengan Statistik Uji z dan Statistik Uji T ? Tulisan selanjutnya klik disini.

Read More......

Statistik Uji z, T pada Model GARCH/ EGARCH dg Eviews

Melanjutkan pertanyaan dari Sohib Mahasiswa di Perguruan Tinggi di Surabaya tentang Pengertian Statistik Uji z dan Statistik Uji T.

Saya mencoba menjawab secara ringkas berkaitan dengan hal itu.

Model GARCH.

Misalkan model GARCH(1,1):

Persamaan pertama adalah mean equation dan persamaan ke dua adalah varians equation. Misalkan Rt adalah first difference Log S&P500 (DLOG(SPX)) dan hasil output Eviews adalah:

Model GARCH tersebut mengasumsikan errornya berdistribusi normal, sehingga untuk menguji signifikansi baik pada masing- masing koefisien pada mean equation maupun varians equation dengan mengunakan statistik uji z. Dengan mengunakan tingkat kesalahan (alpa-5%) maka, semua koefisien baik mean equation maupun varians equation menunjukkan sangat signifikan (p-value kurang dari 5%). Oleh karena itu, perilaku indek S&P 500 dapat dijelaskan dengan model GARCH(1,1).

Model EGARCH.

Misalnya model Exponensial GARCH (1,1):

dimana St=nilai index S&P 500 dan diperoleh output:

bila model EGARCH ini mengasumsikan erorrnya berdistribusi students, maka untuk menguji koefisien pada mean equation dan varians equation dg Statistik Uji z (standarized distribution). Melihat p-value dari statistik uji z masing- masing koefisien pada mean equation maupun varians equation sangat signifikan (lebih kecil dari 5%).

Sadangkan nilai Statistik Uji T-DIST menunjukkan bahwa relative kecil nilai tersebut menununjkkan bahwa distribusi standarized error berasal dari distribusi normal.

Sumber: Eviews User Guide

Read More......